Micro-nano scale heat transfer
As the new generation of semiconductor materials, wurtzite AlN, GaN and InN are widely applied into electronic devices, such as light-emitting diodes (LED) and lasers. The first-principle method, Monte Carlo simulation, molecular dynamic simulation and lattice dynamic method are used to study the heat transport properties in semiconductor materials, e.g. the thermal conductivity of GaN, AlN, InN and their alloys in LED chips and the interface heat transfer.
1. Thermal Conducivity Calculated By the First Principle Method
Heat conduction in crystal is the process of atomic vibrations propagating by interatomic forces. In order to compute the thermal conductivity we need to take the lattice harmonic and anharmonic vibrations into consideration. Normally, the second-order and third-order interatomic force constants are only required to obtain the interatomic anharmonic interactions. The real-space supercell method of the first principle is used to calculate the IFCs, and the phonon Boltzmann transport equation is combined to solve the conductivity.

Fig. 1 Flow chart of the thermal conductivity calculation based on the real-space supercell method.
2. Thermal Conductivity of Wurtzite AlN, GaN and InN
Wurtzite AlN, GaN and InN have the hexagonal lattice structure, which belongs to the P63mc point group space, with isotropic thermal conductivities in the horizontal direction but different values in the vertical direction. We’ve studied the thermal conductivity in both horizontal and vertical directions and use the distinction between values of the two directions to represent the thermal conductivity anisotropy. The thermal conductivity anisotropy for the wurtzite AlN is negligible, so it can be treated as isotropic material. However, large thermal conductivity anisotropy is found in the wurtzite GaN and InN and it becomes stronger with temperature decreased. Relative achievements are published in Appl. Phys. Lett. and J. Applied. Phys..
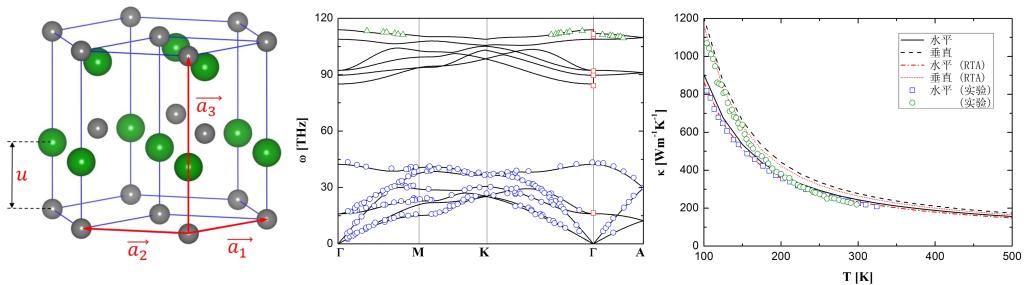
Fig. 2 Schematic of the hexagonal lattice structure of the wurtzite crystal.
Fig. 3 Phonon dispersion relationship of the wurtzite InN in highly symmetric directions.
Fig. 4 Relationship between the wurtzite GaN thermal conductivity and temperature.
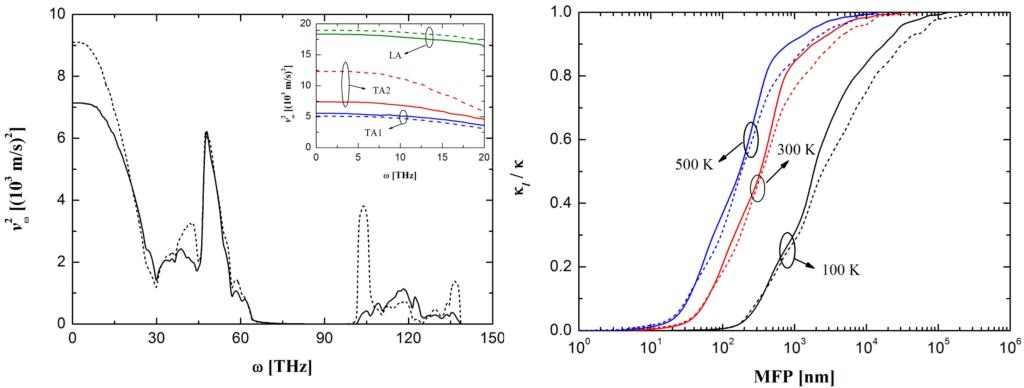
Fig. 5 Distribution of the wurtzite GaN averaged phonon group velocities in the horizontal and vertical directions with frequencies.
Fig. 6 Cumulative function of the wurtzite InN thermal conductivity and the mean free path at various temperatures.
3. Thermal Conductiviy of Wurtzite AlxGa1-xN, InxGa1-xN and InxAl1-xN
Compared to the single crystal, the disordered distributions of different atoms in alloys result in decrease of the lattice symmetric properties, comfinement of the lattice vibration and decrease of the thermal conductivity. It is more challenging for prediction of the thermal conductivity of alloys with disordered systems than that of the pure lattice. Using the virtual lattice model, assume alloys’ disordered lattice structrues to be ordered, having similar lattice structures with the component materials. The corresponding lattice constants and atomic coordinates are the weighted averages by the concentration of the lattice parameters of each component. We obtained the relationship of thermal conductivity of wurtzite AlxGa1-xN, InxGa1-xN and AlxIn1-xN with the component concentration at 300K. Relative achievements are published in Phys. Rev. B and so on.
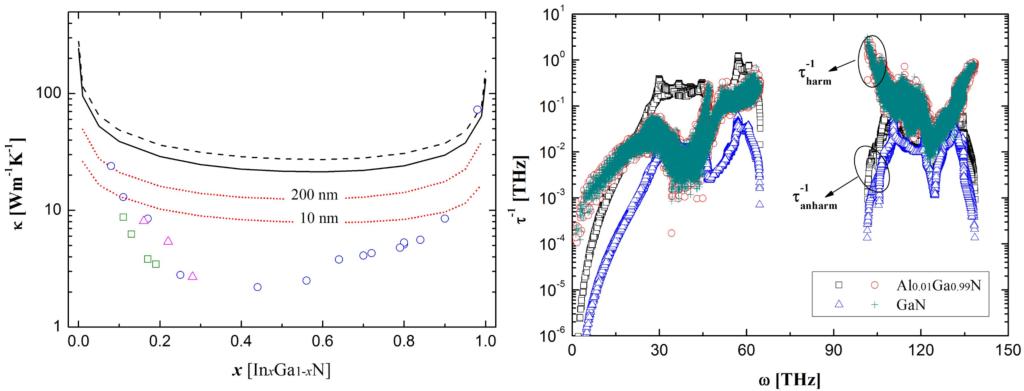
Fig. 7 Relationship between the component concentration and the wurtzite InxGa1-xN thermal conductivity in the horizontal (solid line) and vertical (dash line) directions.
Fig. 8 Distribution function of the harmonic and anharmonic scattering rates of the wurtzite GaN and Al0.01Ga0.99N with frequencies.
Representative papers:
1) Jinlong Ma, Wu Li, Xiaobing Luo*, Intrinsic thermal conductivities and size effect of alloys of wurtzite AlN, GaN, and InN from first-principles, Journal of Applied Physics, Vol:119(12),125702-1-5,2016.
2) Jinlong Ma, Wu Li, Xiaobing Luo*, Ballistic thermal transport in monolayer transition-metal dichalcogenides: Role of atomic mass, Applied Physics Letters, Vol:18(8),082102-1-5,2016.
3) Jinlong Ma, Wu Li*, and Xiaobing Luo*, Intrinsic thermal conductivity and its anisotropy of wurtzite InN, Applied Physics Letters, 105, 082103, 2014.
4) Jinlong Ma, Wu Li*, and Xiaobing Luo*, Examining the callaway model for lattice thermal conductivity, Physical Review B, 90, 035203, 2014.
5) Jinlong Ma, XinJiang Wang, Baoling Huang*, and Xiaobing Luo*, Effects of point defects and dislocations on spectral phonon transport properties of wurtzite GaN, Journal of Applied Physics, 114, 074311 (2013).



